클러스터링이란? (군집화)
- 분할기법(Partitioning methods)
n개의 객체 혹은 튜플이 주어졌을 때, 분할기법은 k가 n보다 작거나 같은 군집을 나타내는 데이터 분할을 k개 만든다. 즉, 데이터를 다음 두가지 조건을 만족하도록 k개의 그룹으로 구분짓는 것이다.
n개의 객체 혹은 튜플이 주어졌을 때, 분할기법은 k가 n보다 작거나 같은 군집을 나타내는 데이터 분할을 k개 만든다. 즉, 데이터를 다음 두가지 조건을 만족하도록 k개의 그룹으로 구분짓는 것이다.
1) 각 그룹은 적어도 하나의 객체를 가져야 함.
2) 각 객체는 정확히 1개의 그룹에 속함.
2) 각 객체는 정확히 1개의 그룹에 속함.
다음에 설명할 처음의 두 클러스터링인 k-Mean, k-Medoids의 클러스터링 방식이 분할기법을 잘 보여준다.
1> k-Mean 클러스터링
-각 군집이 군집에 있는 객체의 평균값으로 대표되는 k-means 알고리즘을 이용함.
-각 군집이 군집에 있는 객체의 평균값으로 대표되는 k-means 알고리즘을 이용함.
> iris2 <- br="" iris="" nbsp="" style="box-sizing: border-box;">> iris2$Species <- 5="" br="" nbsp="" null="" style="box-sizing: border-box;">> (kmeans.result <- 3="" iris2="" kmeans="" nbsp="" span="">
> table(iris$Species, kmeans.result$cluster) # 실제로 클러스터링 결과를 비교해보고자 테이블을 생성하여 비교 -
> plot(iris2[c("Sepal.Length", "Sepal.Width")], col = kmeans.result$cluster) #
# plot cluster centers - 아래수식은 각 클러스터의 중심을 점으로 그리는 것이다. centers는 각 클러스터별로 각 컬럼의 평균값을 나타낸 것이다. 이것에서 우리가 원하는 컬럼값 2개를 선정하였다. col은 색, pch은 모양, cex은 크기를 의미 한다.
> points(kmeans.result$centers[,c("Sepal.Length", "Sepal.Width")], col= 1:3, pch=8, cex=2)
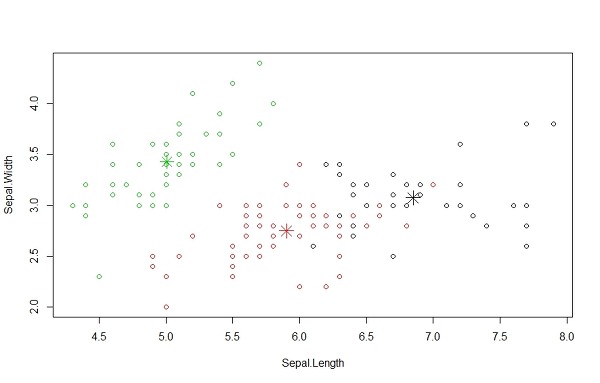
2> k-Medoids 클러스터링
각 군집이 군집의 중앙(중앙값)에 가장 가깝게 위치해 있는 객체 중 하나로 대표될 때, k-medoids 알고리즘을 적용. 이 함수는 앞서본 k-Means 알고리즘보다 특이값이 대해서 안정적인 결과를 얻게 해준다. 하지만 이것을 구현한 PAM함수는 큰 데이터의 경우에 비효율적이라서, 큰 데이터의 샘플을 가져와서 각 샘플에 PAM (Partitioning Around Medoids) 함수를 적용해 최선의 결과를 반환하는 CLARA 알고리즘이 유용하다.
pam(), clara()함수는 cluster 패키지에 포함됨. pamk()는 fpc패키지에 포함됨.
코드를 통해서 pam() 함수와 pamk() 함수의 차이를 알아보겠다.
> install.packages("fpc") # 패키지 인스톨
> library(fpc) # 인스톨한 패키지를 불러오기
> pamk.result <- iris2="" nbsp="" p="" pamk.result="" pamk="">
# number of clusters
> pamk.result$nc # 얻을 결과중에서 클러스터의 개수 확인하기(the number of clusters)
클러스터의 개수가 2개로 나왔다. 아래 코드를 실행시키면 실제 데이터와 비교하여 어떻게 클러스터링이 되었는지 테이블 형식으로 확일 할수 있다.
#check clustering against actual species
> table(pamk.result$pamobject$clustering, iris$Species) # 테이블을 보자.
> layout(matrix(c(1,2), 1, 2)) # 한 화면에 두개의 그래프가 나오도록 설정.
> plot(pamk.result$pamobject) # plot을 그리기.
> layout(matrix(1)) # 한 화면에 한그림만 나오도록(원래대로) 재설정
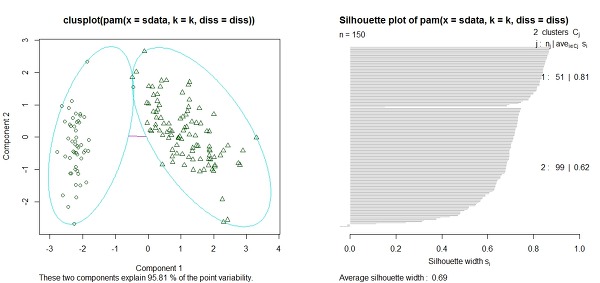
위 그림의 좌측은, iris 데이터를 2개의 클러스터로 나눈것을 보여준다. 가운데 있는 선은 두 클러스터간의 거리를 눈으로 보여준다. iris 데이터의 실루엣(silhouette)을 보여준다. 각 군집은 3가지로 설명되어 있다. 위쪽을 기준으로 설명해보자. 1은 클러스터의 이름이다.(첫번째 클러스터라는 의미) 51은 이 클러스터에 속해있는 점들의 개수이다. 뒷자리의 0.81은 이 클러스터가 잘 모여 있는지 알려준다. 1에 가까울수록 잘 클러스터화 되어 있는것이고 0 주변은 두 군집 사이에 놓여 있는 점을 말하며, 음수로 나타나면 잘못된 클러스터에 속해 있을 가능성이 높다. 실제로 오늘쪽 그래프의 맨 아래쪽 바를 보면 0보다 작은 값으로 막대그래프가 향하고 있음을 발견할 수 있다.
이제는 pam()함수를 사용해보자.
> pam.result <- 3="" iris2="" nbsp="" p="" pam="">
> table(pam.result$clustering, iris$Species) # 테이블로 실제로 클러스터가 각 점이 배치된것을 확인
> layout(matrix(c(1,2), 1,2)) # 한 화면에 두개의 그래프가 나오도록 설정.
> plot(pam.result) # 그래프 그리기
> layout(matrix(1)) # change back to one graph per page
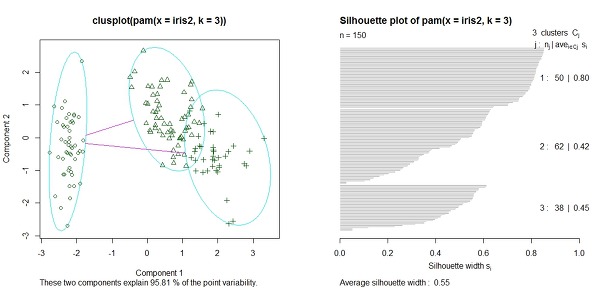
pam() 함수는 앞서 말한것 처럼 내가 몇개의 클러스터를 만들것인지 정할수 있다.
앞선 두 함수중에서 어떤 함수가 더 낫다고 말하기는 어렵다. 해결코자 하는 문제와 해당분야 지식과 경험에 따라서 다르기 때문이다. 앞선 경우에는 우리가 임의로 3개로 클러스터를 정한 것이 더 나은 결과를 얻을 수 있었다. 다시말하면 pam()가 편리하지만 항상 최고의 결과를 보장해주지는 않는다.
3> Hierarchical 클러스터링 (계층화)
계층화를 하는 방식에는 2가지 방식이 있다.
1) agglomerative(집괴적) : 상향식 : 각 객체들 모여서 그룹을 형성함부터 점점 커짐
2) divisive(분할적) : 하향식 : 덜 비슷한것들끼리 분할해 나간다.
우리가 볼 함수는 hclust이다. 이번에도 iris 데이터를 이용하지만, 150개는 너무양이 많은 관계로 40개만 이용해 보려고 한다. 그리고 역시 종(Species)를 제거하고, 함수를 이용해 계층화 한 것이 실제와 어떻게 같거나 다른지 살펴본다.
> idx <- 1="" 40="" dim="" iris="" nbsp="" p="" sample="">
> irisSample <- idx="" iris="" nbsp="" p="">
> irisSample$Species <- nbsp="" null="" p="">
> hc <- dist="" hc="" hclust="" irissample="" method="ave" nbsp="" p="" row="">
> plot(hc, hang=-1, labels=iris$Species[idx]) # 그래프를 그린다. hang은 마지막 내리는 선의 길이를 표현한다.
# cut tree into 3 clusters
> rect.hclust(hc, k=3) #그려진 모양에 맞춰서 빨간색으로 클러스터를 표현합니다. k=3 이면 3개의 클러스터로 표현합니다.
> groups <- 3="" cutree="" hc="" k="3) " nbsp="" p="">
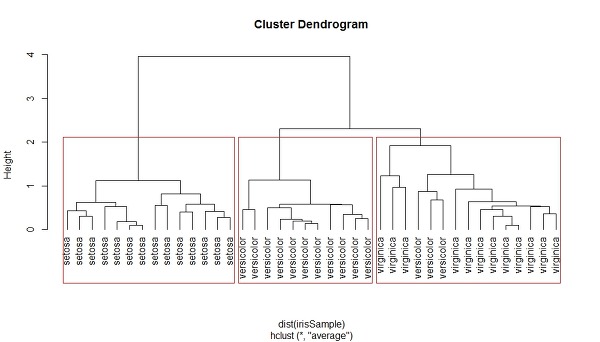
위 그림을 보면, 우리는 세 클러스터로 데이터가 나뉘어 졌음을 알수 있다. 왼쪽은 세토사가 들어있고, 가운데는 versicolor 가 있고, 오른쪽에는 versicolor와 virginica가 섞여 있음을 알수 있다.
이 그래프의 장점은, 만약 내가 4개나 5개등 다른 갯수의 그룹으로 나누고 싶다면 어떻게 나뉘어질지 예측할 수 있다는 것이다.
이 그래프의 장점은, 만약 내가 4개나 5개등 다른 갯수의 그룹으로 나누고 싶다면 어떻게 나뉘어질지 예측할 수 있다는 것이다.
4> Density-based 클러스터링
주어진 클러스터 내에서 각 데이터 포인드들이 주어진 반경 근처에 최소한의 개수는 가지도록 한다. 즉, 근처(neighborhood)의 밀도가 어느 한계점을 능가할 때까지 커진다. 밀도기반 클러스터링은 객체간의 거리에 기초한 대부분의 분할 기법과 다른다. 분할 기법은 보통 구형의 군집만을 찾기때문에 임의의 형태의 군집을 찾는데 어려움이 있다. (예)s자 모양의 군집등. 따라서 임의의 군집을 찾기 위해 밀도기반의 군집화 기법이 발전하였다.
밀도기반 알고리즘은 DBSCAN을 사용하는데 fpc 패키지에 들어있다. DBSCAN에는 두가지 파라미터들이 들어있다.
eps : 도달 가능한 거리. 이것은 이웃들의 크기를 정의한다.
MinPts: 거리내에 있어야만 하는 최소 점들의 개수.
> library(fpc) # 라이브러리 불러오기
> iris2 <- iris="" nbsp="" p="">
> ds <- dbscan="" eps="0.42," iris2="" minpts="5)</p">
# compare clusters with original class labels
> table(ds$cluster, iris$Species) # 실제로 어떻게 분할 되었는지 살피기
그런데 여기서 클러스터 0의 의미는 좀 색다르다. 어떠한 특정 군을 이야기 하는 것이 아니고 아무곳에도 할당되지 않는 것을 검정 동그라미에 할당하였다.
> plot(ds, iris2) # 그래프 그리기. 각 열을 한꺼번에 비교
> plot(ds, iris2[c(1,4)]) # 위 그래프에서 1째 컬럼, 4번째 행렬을 가져옴
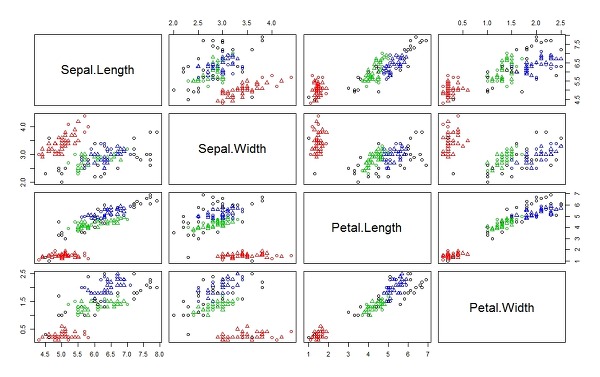
> plotcluster(iris2, ds$cluster) # plotcluster 함수(fpc 패키지에서 가져옴).
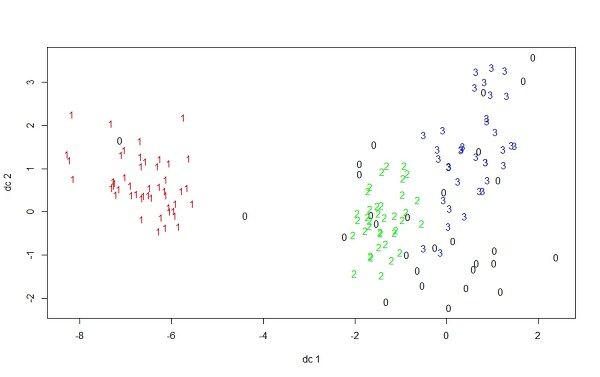
위 그림에서 3개의 클러스터로 구분했음에도 0이 있는 이유는 이것들은 위3개의 클러스터 중, 어느 곳에서 할당되어 있지 않기 때문이다.
새로운 데이터가 들어왔을때 어느 클러스터에 속하는지 한번 보겠다.
# create a new dataset for labeling
> set.seed(435) # 랜덤을 고정시킴
> idx <- 1-150="" 10="" br="" iris="" nbsp="" nrow="" sample="" style="box-sizing: border-box;">> newData <- -5="" br="" idx="" iris="" nbsp="" species="" style="box-sizing: border-box;">> newData <- matrix="" max="0.2)," min="0," ncol="4) " newdata="" nrow="10," runif="" span="">
> idx <- 1-150="" 10="" br="" iris="" nbsp="" nrow="" sample="" style="box-sizing: border-box;">> newData <- -5="" br="" idx="" iris="" nbsp="" species="" style="box-sizing: border-box;">> newData <- matrix="" max="0.2)," min="0," ncol="4) " newdata="" nrow="10," runif="" span="">
#label new data
> myPred <- class="" ds="" iris2="" nbsp="" newdata="" p="" predict="">
# plot result
> plot(iris2[c(1,4)], col=1+ds$cluster) # 그래프로 그리기. 클러스터가 0이 있어서 +1을 함.
> points(newData[c(1,4)], pch="*", col=1+myPred, cex=3) # 새로운 데이터가 어느 군집에 포함되는지 *모양으로 표시해줌
> points(newData[c(1,4)], pch="*", col=1+myPred, cex=3) # 새로운 데이터가 어느 군집에 포함되는지 *모양으로 표시해줌
# check cluster labels
> table(myPred, iris$Species[idx]) # 새로운 군집은 어떠한 테이블을 가지고 있는지 알려줌
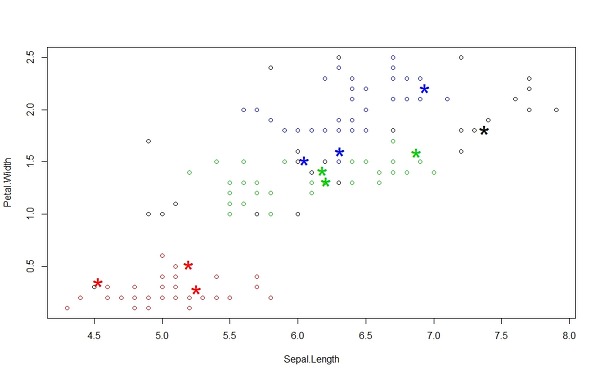위 그림처럼 새롭게 들어온 데이터는 근처에 속한 클러스터의 색에 따라서 할당되어 같은 클러스터로 배정되는 것을 볼수 있다.
도움이 되셨나요?^^
No comments:
Post a Comment